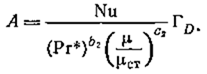Расчёт смесителей. Подбор мешалки

Количественный анализ процесса смешения низковязких сред связан с определением мощности, расходуемой на смешение, времени, необходимого для получения однородной смеси, и теплоотдачи к стенке аппарата.

Критериальное уравнение затрат мощности в геометрически подобных аппаратах с мешалками, при работе которых не происходит образования воронки, часто записывают в виде:

K_N=С(Re_ц^*)^?

Экспериментальные исследования работы различных аппаратов с ньютоновскими и неньютоновскими средами позволили найти значения опытных коэффициентов С и ?, входящих  в критериальное уравнение.

Из рисунка видно, что значения по мощностным затратам на перемешивание ньютоновских жидкостей и неньютоновских сред, показанные критериальным уравнением, в ламинарной и турбулентной областях почти совпадают. Небольшую  разницу можно заметить в области переходного режима, где значение критерия мощности для неньютоновских сред несколько ниже.

Критериальное уравнение для определения времени гомогенизации tм при перемешивании неньютоновских сред различными аппаратами с мешалками обычно представляют в виде:

t_мn=C₁(e_ц^*) ^?1

С учетом влияния геометрических параметров аппарата на характер процесса критериальное уравнение времени гомогенизации может быть записано следующим образом:

t_Mn=?(Reц*,Г_i)

где Г_i — геометрические симплексы.

В основном геометрические симплексы и их воздействие на время смешения устанавливают экспериментально и представляют в форме степенных зависимостей. Однако анализируя простые модели движения жидкостей в аппаратах с мешалками, можно получить аналитические выражения для определения геометрических функций. Определение этих функций базируется на представлении времени циркуляции жидкости в аппарате
t_ц =5t_?, которое находится из расчетов основных потоков, вызванных данной конструкцией мешалки. При этом смеситель рассматривается как центробежный или поршневой насос.

Ниже приведены зависимости для определения геометрических функций для аппаратов с различными перемешивающими устройствами:

турбинное (d_M<<D; b<<D; b= const, где b — ширина лопасти; ? — угол закрутки лопасти; Н — высота жидкости над дном сосуда)

пропеллерное (d_M<<D; b<<D; b= const, ?= const, ??0, ???/2, где ? —угол закрутки лопасти; b — ширина лопасти; h — расстояние от дна аппарата до мешалки)

шнековое (?=const — угол подъема винтовой линии; z — число витков)

ленточное (?=const, d_o — внутренний диаметр мешалки)

Учет геометрических функций значительно сказывается на точности определения времени смешения.

Кроме того, учет геометрических функций позволяет обобщить экспериментальные данные, полученные различными авторами. С помощью диаграммы, приведенной на рисунке, можно решить две основные технологические задачи: для существующего аппарата определенного типа (геометрическая функция известна) можно найти время смешения в зависимости от числа Рейнольдса; для вновь создаваемой конструкции по заданному времени смешения и числу Рейнольдса можно отыскать геометрическую функцию, т. е. определить оптимальные геометрические параметры аппарата с мешалкой.

Следует отметить, что при смешении неньютоновских сред, какими являются, например, полимерные материалы, зависимость t_Mn/?(Г,?)=const оправдывается лишь при больших числах Re_ц*. В ламинарной и переходной областях она существенно зависит от реологических характеристик среды. Это происходит потому, что скорость смешения значительно зависит от скорости сдвига, которая в случае ньютоновских сред будет отличаться при одинаковых условиях. Известно, что при смешении псевдопластичных сред, реологическое действие которых определяется степенным законом, скорость сдвига при увеличении расстояния от оси мешалки падает быстрее, чем для ньютоновских, а при постоянном радиусе увеличивается для сред с большим значением индекса течения. Рост индекса течения ведет также к расширению зоны интенсивного воздействия мешалки.

По мнению многих авторов в непосредственной близи от мешалки для определения скорости сдвига можно воспользоваться приближенной зависимостью =Аn, где А—характеристичеcкая величина для данного типа аппарата. Так для турбинного и пропеллерного аппаратов при D/d_M?1,5 А=11. Если скорость сдвига рассчитать из экспериментально определяемых кривых течения реальных материалов, то выражение для числа Рейнольдса можно представить в виде:

и таким образом учесть неньютоновское поведение смешиваемой среды в непосредственной близи от мешалки. Однако, сделать вывод о характере влияния смесительного органа на весь объем аппарата не представляется возможным.

Цлокарник  установил, что время смешения в аппаратах с ленточной мешалкой обратно пропорционально площади поверхности мешалки. Это обстоятельство должно выполняться и для других типов перемешивающих устройств, действия которых распространяются на весь объем смеси (шнековые, якорные и др.). Безразмерная характеристика, учитывающая это влияние может быть записана в виде зависимости:

(F_M/F_C)^m=?

где F_M и F_C— площадь поверхности мешалки и сосуда.

С уменьшением индекса течения m зона воздействия мешалки на объем сокращается, т. е. увеличение отклонения реологического поведения среды от ньютоновской снижает эффективность смесительного воздействия рабочего органа.

Таким образом, зависимость времени смешения от числа Рейнольдса с учетом геометрических функций и неньютоновского характера поведения среды для различных перемешивающих устройств запишется в виде:

турбинные и пропеллерные

шнековые и ленточные

Учитывая величину ? можно значительно приблизиться к результатам экспериментальных данных различных авторов.

Сравнительная независимость времени смешения от ? при m?1  доказана опытным путем для турбинных, пропеллерных и некоторых других типов перемешивающих устройств. В дилатантных средах надо учесть эффект образования жесткого ядра вокруг мешалки, что затрудняет расчет времени смешения.

Критериальное уравнение теплоотдачи перемешиваемых неньютоновских сред к стенке имеет вид:

где ? и ? — коэффициенты теплоотдачи и теплопроводности; ? — плотность

материала; с_Р — теплоемкость; ? и ?_ст—реологические константы; С₂, ?₂, b₂ и с — константы.

Средняя температура стенки определяется как средняя по поверхности

где TСТ1,  TСТ2, TСТ3, …, TСТn —измеренные значения температур стенки; ?1, ?2 ,?3, … ?n — площади участков поверхности стенки, с площадью поверхности теплообмена F.

Количество переданной теплоты Q_П может быть найдено из зависимости

Q_П= G_BC_B(T_ВХ -T_ВЫХ)

где G_B —расход охлаждающей воды; с_в — теплоемкость воды; Т_вх и Т_вых-— температура воды на входе и выходе.

Коэффициент теплоотдачи ? находят из уравнения:

где T_ср— температура смешиваемой среды.

После этого рассчитывают критерии Рейнольдса Re_ц^*=?n^2-md²_M(4?)^1-m/?, Нуссельта Nu=?d_M/?, Прандтля Рr* =c?n^m-1(4?)^m-1/? и модифицированную поправку Зидера-Тэйта ?/?_С?. Характеристики жидкости, входящие в критерии, находят для средней температуры перемешиваемой среды.

Значения коэффициента С₂ и показателей ?₂, b₂, с для различных типов аппаратов с мешалками приведены на рисунке.

Для расчета потребляемой мощности, времени гомогенизации и теплоотдачи при перемешивании неньютоновских сред мешалками других типов можно использовать в качестве первого приближения уравнения, полученные для ньютоновских сред.